A Closer Look At The WinDaq Derivative Algorithm
The derivative is a mathematical tool used to obtain the rate of change from any given function. When the function to be differentiated is expressed as an equation, we would apply the appropriate derivative formula to attain the rate of change in a similar equation format. When the function is a waveform, an electronic device called a differentiator amplifier can be used to calculate the derivative of the input signal. The result is a second waveform which may be recorded, digitized, or otherwise used to provide additional information about the original waveform.
In a computer-based instrumentation environment, it is possible to differentiate a waveform previously recorded to disk by passing the waveform through a derivative function constructed in software. This latter approach has several advantages. Unlike its hardware counterpart, a software differentiator is driftless, yielding enhanced accuracy and repeatability. Calibration of the resulting differentiated waveform is automatic, in units of the input waveform divided by seconds. Finally, where a hardware solution generates one, take-it-or-leave-it derivative signal, the software differentiator allows enhanced flexibility through multiple derivative operations performed on the same, or a different channel. Each operation can have its own set of parameters providing a valuable "what if" approach to waveform analysis.
This application note seeks to explore the intricacies of software-based waveform differentiation using the derivative utility of DATAQ Instruments' Advanced CODAS analysis package as its model. All elements of waveform differentiation discussed in this piece are incorporated in this product.
Differentiation and Integration Basics
The relationship between differentiation and integration is so close that discussing one naturally leads to a discussion of the other. One of the more fundamental applications of these powerful tools is units transformation. For example, suppose we're acquiring the velocity waveform from an automobile calibrated in feet per second (ft/sec). Using this signal, we can determine the speed of the car at any instantaneous point during the entire test. Useful information, to be sure. But suppose we're curious about the acceleration of the vehicle. In other words, we want the rate of change of the velocity waveform with respect to time. Such information is provided by the derivative function by transforming a waveform calibrated in ft/sec into one calibrated in ft/sec/sec, or ft/sec2. Similarly, we could choose to integrate the velocity waveform to derive a measure of displacement. Following this operation, units are converted from ft/sec to (ft/sec) × sec, or simply "feet".
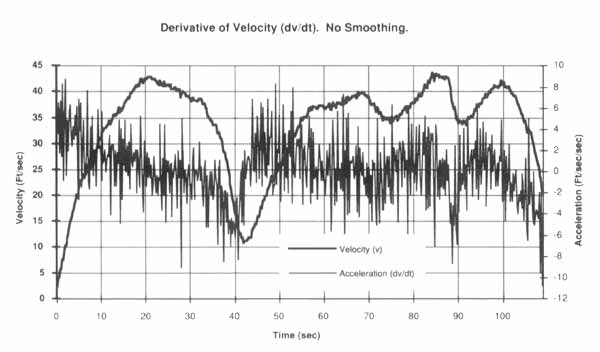
Figure 1 — Applying a derivative function without benefit of smoothing yields a noisy result that provides little information regarding the true rates of change of the input waveform.
Generating a Differentiated Waveform
Turning again to our example velocity waveform and our need to derive acceleration, we could determine the change in velocity over any given range and divide by elapsed time for a rough approximation. But this is a tedious approach to waveform differentiation that can easily lead to errors, and fails to provide an overall graphic picture of acceleration that could help us identify other areas of interest. These problems can be solved by the software differentiator. The most basic approach such products could use to derive the first derivative of a waveform is to calculate the difference between any given point on the velocity waveform, and the next adjacent sample. This difference would then be divided by the elapsed time increment separating the two points to yield the rate of change in units of ft/sec2, or acceleration. The problem with this approach is that the result is extremely noisy as can be seen from Figure 1 which is a simulation of this approach to differentiation. Real world signals always have a noise component which becomes greatly magnified by the process of differentiation. Although the velocity waveform of Figure 1 appears reasonably noise-free, the derived acceleration waveform is virtually useless. Just as analog differentiators provide selectable low-pass filters, so must software differentiators provide a means for smoothing the generated waveform. Many smoothing approaches exist, but the best would be one that combines smoothing with a derivative function leading to more efficient software execution. A least squares algorithm satisfies this requirement.
Least squares as applied to linear regression is a well known technique used for deriving a predictive equation of the form.
y = mx + b
from a randomly sampled group. From basic calculus, we know that the first derivative of this equation (dy/dx) yields m, the slope or rate of change of the line. For differentiation purposes, the intercept quantity (b) is meaningless and therefore not calculated. Armed with this basic information and applying a least squares linear regression model to consecutive points defining an acquired waveform, we can construct an equation for the best-fit line defining these points where m, or slope of the line represents the average rate of change of the line over the waveform values used for the calculation. Extending this reasoning one step further, if we vary the number of points (n) over which the regression line is calculated we can adjust the degree of smoothing that is applied to the calculated rate of change. Higher values of n produce greater smoothing, lower values less smoothing.

Figure 2 — A derivative waveform is generated by calculating the slopes of overlapping line segments comprised of sampled values.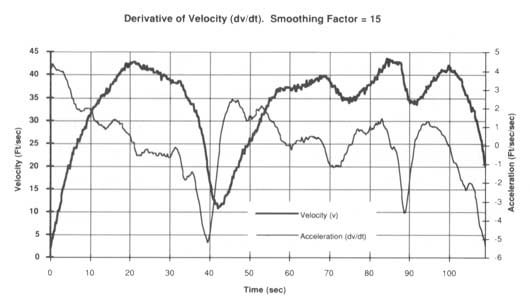
Figure 3 — Smoothing of the derivative waveform can dramatically enhance its readability. Here, a smoothing factor of 15 is applied to the same derivative function shown in Figure 1.
Figure 2 graphically demonstrates how the regression model is applied to waveform data points represented by y. The example uses a smoothing factor of 3, meaning that the slope of each line segment (m), is calculated over 3 consecutive waveform values. Note the overlap that exists in line segment calculations which yields the same number of points in the differentiated waveform as existed in the waveform represented by function y. Figure 3 is the result of applying the regression method to the same velocity waveform of Figure 1. The number of points over which each regression line was calculated is 15, yielding the dramatic degree of smoothing shown in the resulting acceleration waveform.
Figure 4 is a reproduction of a print screen from the playback utility of WinDaq. The top waveform is velocity as acquired from an automobile running on a test track. The bottom waveform is a calculated channel, acceleration, which was derived by taking the first derivative of velocity with a smoothing factor of 15.
Other Waveform Differentiation Issues
There are a number of issues you should consider when choosing an analysis package to perform waveform differentiation. First, make certain that the generated waveform is scaled into meaningful engineering units automatically. The units to which the generated waveform should be scaled are the original waveform units divided by time (usually in seconds). Such capability dramatically simplifies differentiation operations.
Second, waveform differentiators should not require a math co-processor to accelerate computational speed. Such a requirement is a by-product of lazy programming, and simply hangs another cost burden on your system.
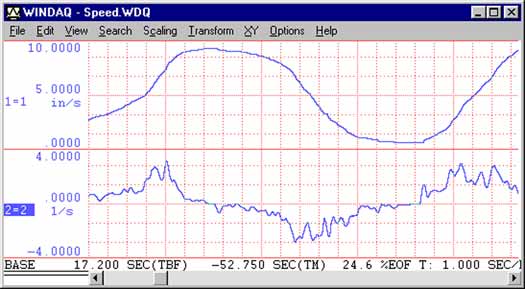
Figure 4 — This reproduction of an WinDaq Playback screen shows the velocity waveform of Figures 1 and 3 in the top window, and the acceleration waveform calculated by Advanced CODAS in the bottom window. A smoothing factor of 15 was applied to the derivative function.
The differentiator should perform calculations using fast, integer math where a co-processor does not offer an advantage. The only floating-point operation required is the single step of calculating a scaling constant which will be used to scale the derivative waveform into meaningful units when required.
Finally, check the data space memory requirements of your analysis package. Some analysis software utilities require that the waveform to be operated on reside entirely in semiconductor memory. This is no problem if the waveform to be analyzed is only 10Kb in length, but could be a real problem when attempting to tackle a 2Mb or larger channel. To insulate yourself from such problems, look for an analysis package that is disk-based. Such systems stream the waveform to be analyzed off disk, through the differentiator, and back to disk as a calculated channel. The only limit to the size of waveform information that can be analyzed using this approach is the size of the hard drive.


 View Cart
View Cart sales@dataq.com
sales@dataq.com 330-668-1444
330-668-1444