A Closer Look at Waveform Integration with Advanced CODAS
Mathematics has relied on the integration function for centuries as an aid to understanding the interrelationships of physical measurements. For example, an integral (or area under the curve) function can be applied to achieve units transformation. A velocity equation may be integrated to derive an equation for displacement; or an acceleration equation integrated to derive velocity. Similarly, a measure of work may be derived by integrating a function to yield a relative gage of activity. Most of us, having been exposed to calculus to some degree, understand the application of integration to equations in a purely mathematical sense. However, application of the integral function to waveforms represents a more abstract use of the tool that is not treated in the general curriculum of calculus courses. Such application knowledge is gained only through experience and it is the intent of this application note to convey a portion of this expertise to shorten the learning curve.
The Advanced CODAS waveform analysis option for DATAQ Instruments' WinDaq data acquisition systems contains a waveform integrator that was the model for this application note and embodies all elements of waveform integration discussed herein.
Reset Conditions: The Key To Waveform Integration
The object of a waveform integrator is to generate a waveform of equal length representing the area bounded by the curve of the input signal over a predetermined integration period. The integration period represents the point at which the accumulated area is reset to zero and area accumulation resumes with the next point of the input signal. This reset activity is extremely important to the integration process. In a graphical sense, it allows an integrated waveform of any length to be generated without saturation. In an analysis sense, it allows the integrated waveform to be broken down into meaningful segments.
To clarify these points, consider a velocity waveform generated by an automobile which is integrated to derive displacement. If we assume that the auto always travels in the same direction but at varying speed, the velocity waveform produced will always be above or below zero (depending upon the direction of travel) and will never cross zero, since to do so implies a change of direction. If we further assume that the auto is traveling at a high rate of speed for a long period of time, it should be obvious that total distance traveled can become very large. The integral of velocity representing distance drifts more and more positive (or negative depending upon direction) until saturation occurs. Of course in a digital system, the waveform may be scaled based on maximum distance, but to do so suppresses changes in the displacement waveform at the lower displacement values (i.e., when the auto first started moving).
We can solve these problems by applying reset conditions to the integration of the velocity waveform described above. If we apply a reset condition based on time, say 20 seconds, then the integrated waveform will reset every 20 seconds. The height of the waveform just before reset occurs represents the total distance traveled over the 20 second interval. Since we've segmented the displacement waveform into 20-second epochs, the need to heavily scale the waveform has been eliminated and small variations in the displacement waveform will be evident as an enhancement to analysis.
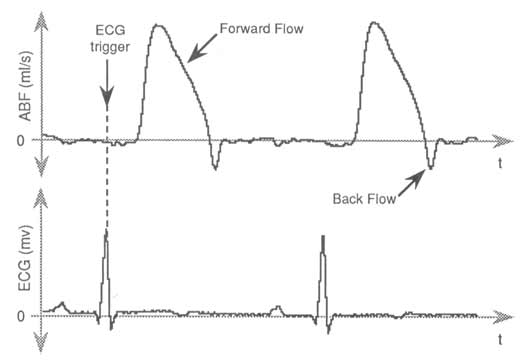
Figure 1 — The anatomy of an aortic blood flow waveform (ABF) contains both positive and negative flow components. ABF is synchronous with the electrocardiogram (ECG) signal; the electrical stimulus that commands the heart to beat.
Let's consider another reset condition based on distance traveled and configure the waveform integrator to reset every 1,000 feet. The resulting displacement waveform will reset at varying times, but immediately upon a travel distance of 1,000 feet. Again, since we've segmented the waveform, the need for scaling has been greatly diminished and any fluctuation in displacement will be apparent.
We can extend the example to include an auto traveling forward and backward and the need to derive forward and backward displacement from the velocity waveform. Here, a reset condition based on zero crossing of the velocity waveform may be appropriate. Since zero velocity must be achieved when a change of direction occurs, integrator reset at this point yields a segmented view of forward and backward displacement.
The application of reset conditions to the waveform integration process provides an element of flexibility and is solely responsible for bringing the power of the integral function to waveform analysis. Several reset methods are typically employed for waveform integration: As a function of zero crossing, level, time, and external event. Each function will be demonstrated in examples that follow.
Rectification Enhances Waveform Integration
In many different applications the waveform integration process is enhanced by the ability to apply rectification as a preliminary step before integration. Consider our example above where the automobile is moved forward and backward and the resulting bipolar velocity waveform is to be integrated to yield displacement. We've used the label bipolar here to describe a velocity signal that is both positive-and negative-going since the auto is moving forward and backward. We'll assume that a forward direction generates a positive velocity waveform.
Suppose you are interested in deriving only positive displacement. The bipolar velocity waveform may be preconditioned before actual integration by applying a half wave rectifier that passes only signal information above zero velocity to the integrator. Similarly, if your interest is only negative displacement, the half wave rectifier may be applied to pass only negative-going velocity waveform information to the integrator. A measure of total displacement can be derived by applying a full wave rectifier (or absolute value) to the velocity signal before integration.
Preconditioning in the form of waveform rectification adds analysis flexibility to the integration task.
Aortic Blood Flow: An Application Example
An unlimited number of waveforms qualify to be used as examples for waveform integration. For this application note, we've chosen a waveform encountered in medical research applications called aortic blood flow (see Figure 1) because it offers so many possibilities for waveform integration. The typical unit of measure for this waveform is milliliters per second (ml/s). As its units imply, aortic blood flow (ABF) may be thought of as a velocity waveform similar to feet per second or miles per hour. When integrated, the ABF waveform yields a measure of blood volume in milliliters according to the equation: (ml/s × s = ml).
Integration Using Zero Crossing Resets
ABF waveform area above 0 ml/s represents forward volume; the quantity of blood pumped away from the heart. Waveform area below 0 ml/s represents back volume; the quantity of blood pumped toward the heart as a result of the heart valve snapping shut and creating a slight, temporary negative pressure. The bipolar nature of ABF allows application of the rectifier to precondition the waveform before integration to isolate the positive and negative flow components. Further, whenever ABF crosses zero a change of velocity direction has occurred by definition and we can use this characteristic to trigger integration resets. Figure 2 shows how the rectifier may be applied to isolate positive- and negative-going waveform excursions of the input ABF waveform, then apply only these segments to the integrator. The resulting integrated waveforms provide a measure of blood volume pumped in a forward and backward direction during each heart cycle. The reset condition for each integrated output of Figure 2 occurs immediately upon zero crossing of the ABF waveform as detected by the integrator software algorithm.
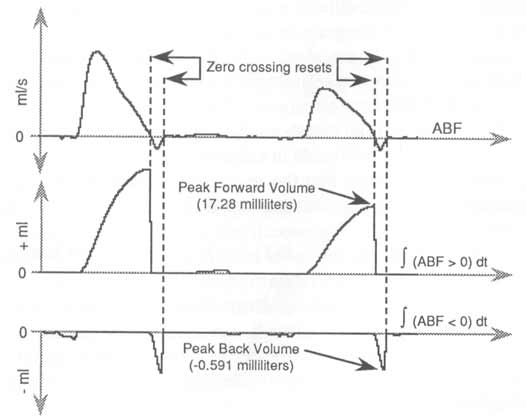
Figure 2 — Applying a built-in waveform rectifier function allows the positive and negative flow components of ABF to be integrated into separate forward and back volume components. In this example, zero crossing of the ABF waveform resets integration.
Integration Using Level, Time, and External Resets
Suppose our interest in the ABF waveform is not to derive the quantity of blood pumped per heart cycle, but how long it takes the heart to pump a given quantity of blood. Zero crossing resets do not apply here. As we've seen, this approach applies only to cycle-by-cycle analysis. To achieve our objective an entirely different reset condition must be applied called level reset. Given a desired level of the integrated waveform it is possible to force a reset condition when that quantity is achieved. The interval between reset conditions represents the time required to achieve the specified level. Turning to our example ABF waveform, specifying a level reset of 10 ml will cause the integrator to reset only when a total of 10 ml of blood is pumped (see Figure 3b). Zero crossings of ABF are ignored.
Time reset is the converse of level reset. Where a level reset derives the amount of time required to achieve a fixed integrated level, a time reset derives the level achieved by the integrated waveform over a fixed time. Turning to Figure 3c, a time reset of 0.5 seconds was enabled, yielding a peak integrated value of 43.3 ml. As with level resets, zero crossings of the ABF waveform are ignored during time reset operations.
Finally, external resets allow you to synchronize reset activity to an external event occurring on the input or any other channel. Consider the piston of an air compressor and the need to measure total work applied during each stroke of the piston. We could mount a pressure transducer at the top of the cylinder and a magnetic pickup on the piston's crankshaft and acquire the signals of both with a data acquisition system. Using another Advanced CODAS software utility referred to as the Peak Detector, we could peak capture the pickup's waveform placing a marker at the peak amplitude of each pickup cycle. The interval between adjacent markers represents one cycle of the piston regardless of crankshaft rotational speed. This "marked" waveform then becomes the synchronized reset condition for the integrated pressure waveform, resetting the integral each time it occurs. The result is a cycle-by-cycle true measure of total work applied by the piston.
Returning to our ABF waveform, remember that it is synchronous with the electrocardiogram (ECG) signal (see Figure 1) with the peak of this waveform representing the electrical stimulus commanding the heart to beat. Peak capturing the ECG waveform and using the resulting markers to reset integration of ABF yields the most accurate measure of beat-by-beat blood volume (see Figure 4b).
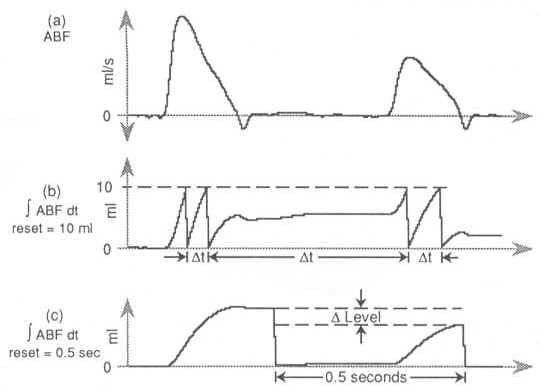
Figure 3 — Reset flexibility is the key to effective waveform integration. The signal ABF (a) produces the waveform shown by (b) which resets when integrated values achieve a level of l 0 ml. Integration resets as a function of time (0.5 seconds) in the waveform shown by (c).
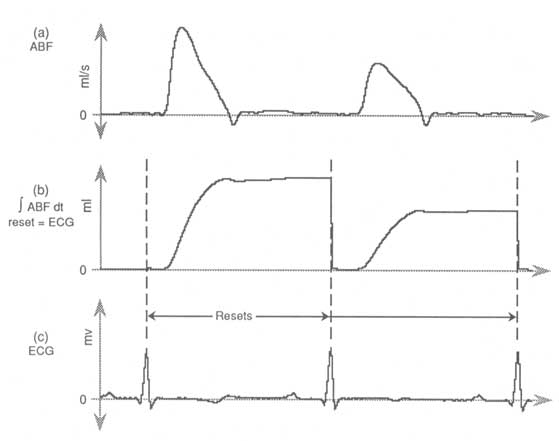
Figure 4 — External reset capability allows waveform integration to reset as a function of a synchronous event. Here, integration of ABF (a) occurs synchronously with the ECG waveform (c) to produce the integrated result of (b) which is the most accurate measure of pumped blood volume per heart cycle.
Other Waveform Integration Issues
Software systems supporting waveform integration should be capable of automatic calibration in the input signal's units times seconds since calibrating an integrated waveform can be a difficult and time-consuming task. In the same vein, the software should accept arguments for the level reset method in units of the output waveform to avoid difficult transformations. For example, a level reset of "1000" kilometers is all that should be required before integrating a velocity waveform calibrated in kilometers per second. Finally, it is extremely important that the reader understand that the terms "zero crossing" and "rectification" applied to a reset condition and pre-integration conditioning respectively, are relative to zero reference of the input signal, not zero volts or A-D counts. Rarely does zero calibrated units of measure relate to zero volts connected to the front end of an A-D system. Input signal offsets are nearly always present and the data acquisition system in use should have the ability to define zero at any point within the dynamic range of the A-D and use this as a calibrated zero reference to detect waveform zero crossings and achieve rectification.
Analysis Beyond Integration
We've discussed some powerful techniques that can be applied to the integration of waveform information. Although viewing an integrated result along with an original waveform can provide insights not intuitively obvious, further data analysis may be applied by extracting cycle-by-cycle peak integrated waveform values and porting these to a spreadsheet or other package for further analysis. DATAQ Instruments' Application Note A Closer Look at the Advanced CODAS Peak Capture Algorithm provides a detailed treatment of how peak captured data can be applied as an aid to data reduction and analysis. This and other application notes are available free-of-charge.


 View Cart
View Cart sales@dataq.com
sales@dataq.com 330-668-1444
330-668-1444