How Much ADC Resolution Do You Really Need?
You just bought a data logger or data acquisition system with a 14-bit ADC (analog-to-digital converter.) What exactly does that mean? Could you have gotten away with a 12-bit product? A 10-bit? Did you gaffe and really need a 16-bit data logger? You know that a higher "bit" number is better, but how much better is "better"? This application note describes a method you can use to answer these questions in terms of your specific situation, as opposed to the generalized explanations provided by product data sheets.
First, some background. The bit value of an analog-to-digital converter refers directly to its resolution. That refers to how finely it slices its full-scale measurement range, or in other words, the smallest change in the input signal that it can theoretically measure (ignoring noise). Using an example we're all familiar with, a ruler calibrated in 1/16th of an inch offers sixteen times the resolution of another calibrated only in whole inches. Depending upon what you're trying to do the higher resolution may be overkill, like measuring the length of your driveway. But it may come in handy for sizing up the miter joints of the dining room cabinet you're building. Likewise, high ADC resolution is sometimes handy and sometimes overkill, but it's more difficult to quantify where the breakpoints are. You have to start with basic information:
- Determine the full-scale input voltage range of the data logger (from the amplifier's input, if one is used); we'll call this VD. Some data loggers offer fixed ranges, and others allow variable ranges. Determine your range in volts and assign it to variable VD.
- Determine the full-scale output voltage range of the signal you want to measure; we'll call this VS. Even if your signal source is a transducer that measures torque, pressure, load, etc. it has a maximum output signal magnitude in volts (or millivolts) that you assign to variable VS. Note that some transducers have a 4-20 mA process current output. I'll deal with that in a special example later.
- Determine what VS represents in terms of engineering units; we'll call this E. A pressure sensor with a 20 mV full-scale output at a full-scale pressure of 10,000 psi assigns a value of 10,000 to variable E.
- Note the bit resolution of the ADC; we'll call this n.
- Determine if your ADC is configured for a bipolar, or unipolar range; we'll call this B. Your data logger has a bipolar range if it can measure signals both above and below zero. It has a unipolar range if can only measure signals that are either above or below zero, but not both at the same time. Set B=1 for bipolar, and B=0 for unipolar.
After you assemble all the above variables for your application, simply plug them into Equation 1 to determine resolution, the smallest change that your data acquisition system can measure in your engineering unit of measure.
EQUATION 1
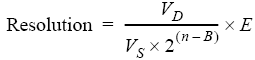
Let's work through some examples.
EXAMPLE 1
Description
Your data logger has a ±10 volt full-scale range (bipolar), and 12-bit ADC resolution. You're connecting a torque transducer that has a 5-volt full-scale output, rated for 100 ft-lbs at full scale.
Variable Assignments
VD = 10VS = 5
E = 100
n = 12
B = 1
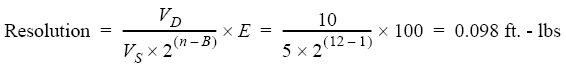
The data logger will not respond to changes in torque of less than 0.098 ft-lbs.
EXAMPLE 2
Description
Same as Example 1, except that the ADC has a unipolar measurement range.
Variable Assignments
VD = 10VS = 5
E = 100
n = 12
B = 0
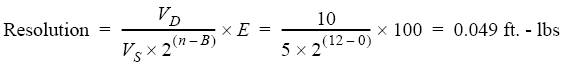
The data logger will not respond to changes in torque of less than 0.049 ft-lbs.
EXAMPLE 3
Description
You have a 100,000 lb. load cell with a gage factor of 1.98 connected to a 2 mV/V amplifier ahead of a 14-bit, bipolar ADC. Assume that the full-scale output range of the amplifier equals the full-scale input range of the ADC.
Variable Assignments
VD = 2VS = 1.98
E = 100,000
n = 14
B = 1
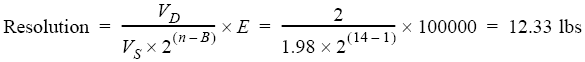
The data logger will not respond to changes in load of less than 12.33 lbs. Note that since we assumed that the full-scale input ranges of the amplifier and the ADC match, we only need to compare amplifier and transducer gage factors for VD and VS respectively.
EXAMPLE 4
Description
You need to measure the 4-20 mA process current output of a distance sensor with a range of 0 to 10 millimeters. You'll use a 250-ohm shunt resistor connected to a 12-bit ADC with a ±5 VFS bipolar range.
Variable Assignments
VD = 5VS = (5-1) = 4
E = 10
n = 12
B = 1
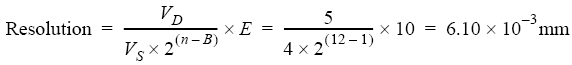
The data logger will not respond to changes in distance of less than 0.0061 mm. Using Ohms Law (V = I × R) we can determine that the voltage across the shunt will range from 1 to 5 volts (V = 0.004 × 250; V = 0.020 × 250 ). This means that only (5- 1) or 4 volts is available for the measurement.
EXAMPLE 5
Description
A pressure transducer with a 1,000 psi range is connected to an amplifier with a 1 volt full-scale output at 1,000 psi. The amplifier is connected to a 12-bit ADC with a ±10 volt full-scale bipolar range.
Variable Assignments
VD = 10VS = 1
E = 1000
n = 12
B = 1
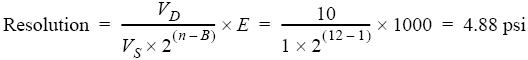
EQUATION 2
Suppose you know how much resolution your measurement needs, but not the bit spec of the ADC that's required to deliver it. Simply rearrange Equation (1) to solve for n, the ADC's bit resolution. Using variable R to represent the desired resolution we get:
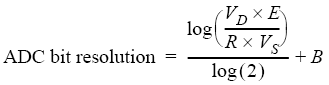
EXAMPLE 6
Description
A pressure measurement demands 0.10 psi resolution or better over a 100 psi full scale range. What ADC bit resolution is required if we amplify the pressure signal to 5 VFS and connect it to an ADC with a ±5 volt full-scale bipolar range?
Variable Assignments
VD = 5VS = 5
E = 100
n = ?
B = 1
R = 0.10
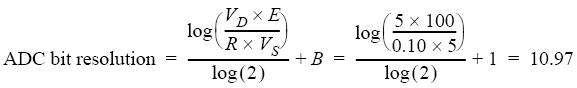
The data logger needs to have a resolution of 11 bits or better to provide a pressure resolution of 0.10 psi.
As a final note, always remember that to gain the complete benefit of your ADC's resolution you must match the full-scale ranges of both the ADC and the signal of interest. We cover this topic in detail in The Fact, Folly and Mathematics of Analog to Digital Converter Resolution.


 View Cart
View Cart sales@dataq.com
sales@dataq.com 330-668-1444
330-668-1444