FFT (Fast Fourier Transform) Waveform Analysis

Order a DI-188 WinDaq starter kit for $49 to study FFT
ExcelLink can stream data to Excel directly to generate FFT
To calculate an FFT (Fast Fourier Transform), just listen. The human ear automatically and involuntarily performs a calculation that takes the intellect years of mathematical education to accomplish. The ear formulates a transform by converting sound—the waves of pressure traveling over time and through the atmosphere—into a spectrum, a description of the sound as a series of volumes at distinct pitches. The brain then turns this information into perceived sound.
A similar conversion can be done using mathematical methods on the same sound waves or virtually any other fluctuating signal that varies with respect to time. The Fourier transform is the mathematical tool used to make this conversion. Simply stated, the Fourier transform converts waveform data in the time domain into the frequency domain. The Fourier transform accomplishes this by breaking down the original time-based waveform into a series of sinusoidal terms, each with a unique magnitude, frequency, and phase. This process, in effect, converts a waveform in the time domain that is difficult to describe mathematically into a more manageable series of sinusoidal functions that when added together, exactly reproduce the original waveform. Plotting the amplitude of each sinusoidal term versus its frequency creates a power spectrum, which is the response of the original waveform in the frequency domain. Figure 1 illustrates this time to frequency domain conversion concept.
The Fourier transform has become a powerful analytical tool in diverse fields of science. In some cases, the Fourier transform can provide a means of solving unwieldy equations that describe dynamic responses to electricity, heat or light. In other cases, it can identify the regular contributions to a fluctuating signal, thereby helping to make sense of observations in astronomy, medicine and chemistry. Perhaps because of its usefulness, the Fourier transform has been adapted for use on the personal computer. Algorithms have been developed to link the personal computer and its ability to evaluate large quantities of numbers with the Fourier transform to provide a personal computer-based solution to the representation of waveform data in the frequency domain. But what should you look for in Fourier analysis software? What makes one software package better than another in terms of features, flexibility, and accuracy? This application note will present and explain some of the elements of such software packages in an attempt to remove the mystery surrounding this powerful analytical tool.
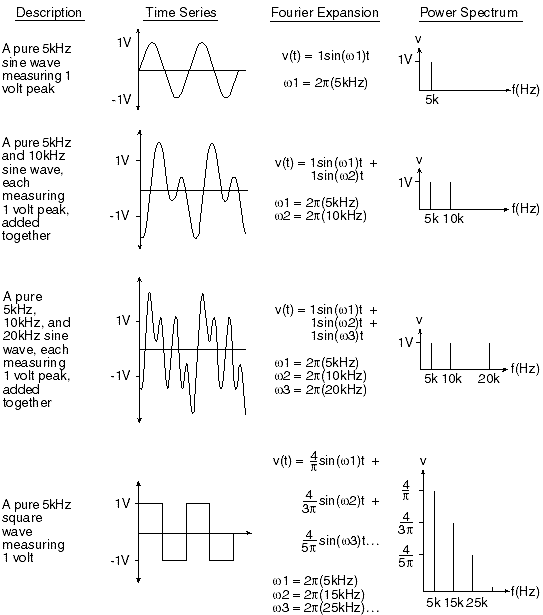
Figure 1 — The Fourier transform illustrated
DATAQ Instruments' WinDaq Waveform Browser (WWB) playback software contains a Fourier transform algorithm that was the model for this application note and includes all elements of Fourier transformation discussed herein. All graphics and concepts presented in this note are also derived from the WWB Fourier transform utility.
A Trio of Transforms
Before computers, numerical calculation of a Fourier transform was a tremendously labor intensive task because such a large amount of arithmetic had to be performed with paper and pencil. These calculations became more practical as computers and programs were developed to implement new methods of Fourier analysis. One such method was developed in 1965 by James W. Cooley and John W. Tukey1 Their work led to the development of a program known as the fast Fourier transform. The fast Fourier transform (FFT) is a computationally efficient method of generating a Fourier transform. The main advantage of an FFT is speed, which it gets by decreasing the number of calculations needed to analyze a waveform. A disadvantage associated with the FFT is the restricted range of waveform data that can be transformed and the need to apply a window weighting function (to be defined) to the waveform to compensate for spectral leakage (also to be defined).
An alternative to the FFT is the discrete Fourier transform (DFT). The DFT allows you to precisely define the range over which the transform will be calculated, which eliminates the need to window. On the negative side, the DFT is computationally slower than the FFT.
The transformation from the time domain to the frequency domain is reversible. Once the power spectrum is displayed by one of the two previously mentioned transforms, the original signal can be reconstructed as a function of time by computing the inverse Fourier transform (IFT). Each of these transforms will be discussed individually in the following paragraphs to fill in missing background and to provide a yardstick for comparison among the various Fourier analysis software packages on the market.
Power Spectrum Generation Using the FFT
The FFT is just a faster implementation of the DFT. The FFT algorithm reduces an n-point Fourier transform to about
(n/2) log2 (n)
complex multiplications. For example, calculated directly, a DFT on 1,024 (i.e., 210) data points would require
n2 = 1,024 × 1,024 = 220 = 1,048,576
multiplications. The FFT algorithm reduces this to about
(n/2) log2 (n) = 512 × 10 = 5,120
multiplications, for a factor-of-200 improvement.
But the increase in speed comes at the cost of versatility. The FFT function automatically places some restrictions on the time series to be evaluated in order to generate a meaningful, accurate frequency response. Because the FFT function uses a base 2 logarithm by definition, it requires that the range or length of the time series to be evaluated contains a total number of data points precisely equal to a 2-to-the-nth-power number (e.g., 512, 1024, 2048, etc.). Therefore, with an FFT you can only evaluate a fixed length waveform containing 512 points, or 1024 points, or 2048 points, etc. For example, if your time series contains 1096 data points, you would only be able to evaluate 1024 of them at a time using an FFT since 1024 is the highest 2-to-the-nth-power that is less than 1096.
Because of this 2-to-the-nth-power limitation, an additional problem materializes. When a waveform is evaluated by an FFT, a section of the waveform becomes bounded to enclose 512 points, or 1024 points, etc. One of these boundaries also establishes a starting or reference point on the waveform that repeats after a definite interval, thus defining one complete cycle or period of the waveform. Any number of waveform periods and more importantly, partial waveform periods can exist between these boundaries. This is where the problem develops. The FFT function also requires that the time series to be evaluated is a commensurate periodic function, or in other words, the time series must contain a whole number of periods as shown in Figure 2a to generate an accurate frequency response. Obviously, the chances of a waveform containing a number of points equal to a 2-to-the-nth-power number and ending on a whole number of periods are slim at best, so something must be done to ensure an accurate representation in the frequency domain. Before we examine a way to ensure accuracy in the frequency domain, lets look closer at the whole/partial number of periods dilemma.
What would happen if an FFT was performed on a waveform that did not contain a whole number of periods as shown in Figure 2b?
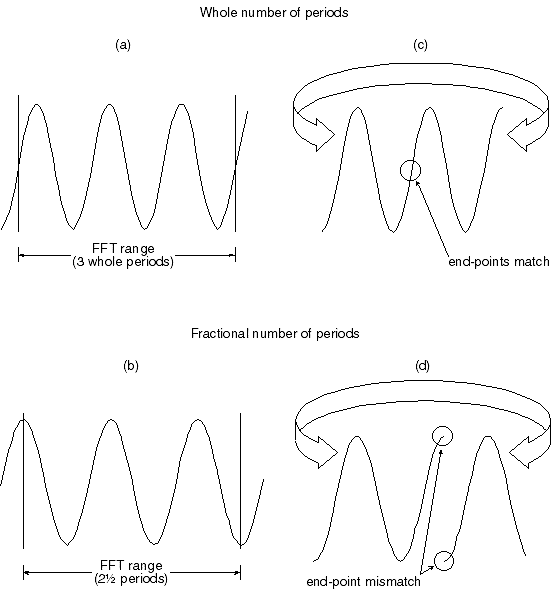 Figure 2 — An example of waveform continuity versus discontinuity that avoids complicated mathematical explanation. (a) shows a best case, one-in-a-million waveform where the range of the FFT exactly contains a whole number of periods, starting with the waveforms mean value. This waveform possesses end-point continuity as shown in ( c), which means the resulting power spectrum will be accurate and no window need be applied. A more typical encounter is shown in (b), where the range of the FFT does not contain a whole number of periods. The discontinuity in the end-points of this waveform (d) means the resulting power spectrum will contain high frequency components not present in the input, requiring the application of a window to attenuate the discontinuity and improve accuracy.
Figure 2 — An example of waveform continuity versus discontinuity that avoids complicated mathematical explanation. (a) shows a best case, one-in-a-million waveform where the range of the FFT exactly contains a whole number of periods, starting with the waveforms mean value. This waveform possesses end-point continuity as shown in ( c), which means the resulting power spectrum will be accurate and no window need be applied. A more typical encounter is shown in (b), where the range of the FFT does not contain a whole number of periods. The discontinuity in the end-points of this waveform (d) means the resulting power spectrum will contain high frequency components not present in the input, requiring the application of a window to attenuate the discontinuity and improve accuracy.
Think of the length of waveform to be evaluated as a ring that has been uncoiled. If the ends of the uncoiled ring were joined back together to again form a ring, a waveform consisting of a whole number of periods would join together perfectly as shown in Figure 2c. However, a waveform consisting of a fractional number of periods would not join together perfectly without a gap between or an overlapping of the ends as shown in Figure 2d. Thus, the FFT would evaluate this waveform with the end-point error and generate a power spectrum containing false frequency components representative of the end-point mismatch. Consider the spectra shown in Figure 3. This figure shows the power spectrum of two sine waves of equal amplitude and frequency. However, the peak of the right power spectrum appears somewhat "spread out". This inaccuracy is the result of an FFT performed on a waveform that does not contain a whole number of periods. The spreading out or "leakage" effect of the right power spectrum is due to energy being artificially generated by the discontinuity at the end points of the waveform.
Fortunately, a solution exists to minimize this leakage effect error and ensure accuracy in the frequency domain. Aside from the DFT (to be defined), the only solution is to multiply the time series by a window weighting function before the FFT is performed. Most window weighting functions (often referred to as just "windows") attenuate the discontinuity by tapering the signal to zero at both ends of the window, as shown in Figure 5d. However, if your waveform has important information appearing at the ends of the window, it will be destroyed by the tapering. In this case, a solution other than a window must be sought. With the window approach, the periodically incorrect signal as processed by the FFT will have a smooth transition at the end points which results in a more accurate power spectrum representation. A number of windows exist. Each has different characteristics that make one window better than the others at separating spectral components near each other in frequency, or at isolating one spectral component that is much smaller than another, or whatever the task. Some popular windows (named after their inventors) are Hamming, Bartlett, Hanning, and Blackman. The Hamming window offers the familiar bell-shaped weighting function but does not bring the signal to zero at the edges of the window. The Hamming window produces a very good spectral peak, but features only fair spectral leakage reduction. The Bartlett window offers a triangular shaped weighting function that brings the signal to zero at the edges of the window. This window produces a good, sharp spectral peak and is good at reducing spectral leakage as well. The Hanning window offers a similar bell-shaped window (a good approximation to the shape of the Hanning window can be seen inFigure 5d) that also brings the signal to zero at the edges of the window. The Hanning window produces good spectral peak sharpness (as good as the Bartlett window), but the Hanning offers very good spectral leakage reduction (better than the Bartlett). The Blackman window offers a weighting function similar to the Hanning but narrower in shape. Because of the narrow shape, the Blackman window is the best at reducing spectral leakage, but the trade-off is only fair spectral peak sharpness. As Figure 4 illustrates, the choice of window function is an art. It depends upon your skill at manipulating the trade-offs between the various window constraints and also on what you want to get out of the power spectrum or its inverse. Obviously, a Fourier analysis software package that offers a choice of several windows is desirable to eliminate spectral leakage distortion inherent with the FFT.
In short, the FFT is a computationally fast way to generate a power spectrum based on a 2-to-the-nth-power data point section of waveform. This means that the number of points plotted in the power spectrum is not necessarily as many as was originally intended. The FFT also uses a window to minimize power spectrum distortion due to end-point discontinuity. However, this window may attenuate important information appearing on the edges of the time series to be evaluated and distort the results of an IFT operation (to be defined) as can be seen in Figure 5d. With these limitations inherent to the FFT, does the Fourier analysis software package you are considering offer a solution other than the FFT?
Another solution abandons windowing in favor of allowing the user to precisely define the range over which the Fourier transform will be calculated. This approach nullifies the 2-to-the-nth-power limitation and is called a DFT.
Power Spectrum Generation Using The DFT
If it is necessary to transform a portion of the waveform with more precision than the FFT will allow, or when a non-windowed transform is desired, DFT generation is the answer. For example, if you are processing transient signals, the edges contain important information that will be unacceptably distorted by applying the window solution. In this case, you would have no choice but to use the DFT. As stated previously, the DFT allows you to adjust the end-points that define the range of the waveform to be transformed, thus eliminating the need for windowing. This approach allows a waveform containing any number of points to be evaluated, which provides more flexibility than the fixed-length, 2-to-the-nth-power FFT. However, to prevent the same leakage effect experienced with a non-windowed FFT, the DFT must be generated over a whole number of periods starting at the waveforms mean level crossing. In other words, the end-points that define the range of the waveform over which the DFT will be calculated must be adjusted to enclose or define a whole number of periods, preferably starting at or around the point where the waveform crosses its mean.
The DFT allows more versatility and precision than the FFT. However, versatility and precision come at the expense of added computation time by the algorithm and added time spent by you on end-point positioning. For example, Table 1 compares the difference in computation time required to generate an FFT and a DFT on an identical waveform using DATAQ Instruments' WWB Fourier transform utility. The times shown are in seconds and were obtained from a 386-based, 25 megahertz PC without a math coprocessor. Since the WWB Fourier transform algorithm uses integer arithmetic, a math co-processor does little to increase performance and is therefore not needed for this package. Some software packages either require a math co-processor for operation or strongly recommend one for optimal performance. Note the DFT computation times are only approximately four times slower than those of the FFT. This is because the WWB utility uses a computational technique very similar to the FFT in order to compute the DFT. The result is a much faster calculation than the standard n2 number of multiplications normally required by a DFT.
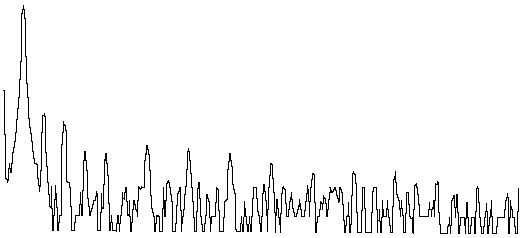
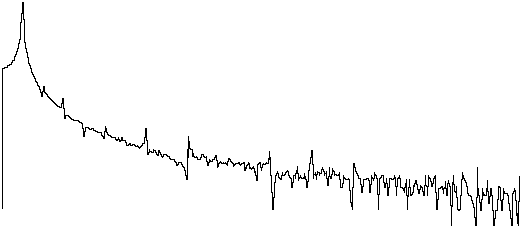 Figure 3 — The spectrum of a sine wave peaks at a single frequency as shown on top in the illustration above when an FFT is performed on a section of waveform that contains a whole number of periods. If the FFT is performed on a fractional number of periods, the spectrum gives a very different picture as shown on the bottom in the illustration above — a broad peak resulting in poorly determined frequency and inaccurate amplitude. These waveforms were generated by an inexpensive function generator, which accounts for the noise present in the spectrum.
Figure 3 — The spectrum of a sine wave peaks at a single frequency as shown on top in the illustration above when an FFT is performed on a section of waveform that contains a whole number of periods. If the FFT is performed on a fractional number of periods, the spectrum gives a very different picture as shown on the bottom in the illustration above — a broad peak resulting in poorly determined frequency and inaccurate amplitude. These waveforms were generated by an inexpensive function generator, which accounts for the noise present in the spectrum.
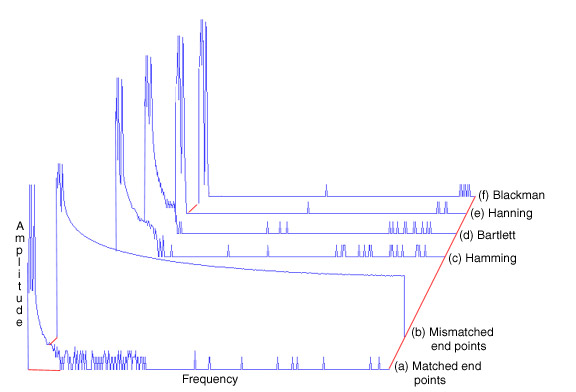 Figure 4 — The significance of window selection is well illustrated by the Fourier transformation of two sine waves close to each other in frequency, but widely differing in amplitude. (a) shows the best case, matched end-point transform where the two signal frequencies that makeup the original waveform are clearly defined, one 2.2 Hz at 90 dB and the other 10.9 Hz at 46 dB. More typically, (b) shows the transform of the same waveform only with mismatched end-points. Note that the second peak is not even visible in this spectrum. The need for a window clearly exists. The remaining transforms illustrate the degree of success attained with various windows in suppressing spectral leakage and recovering the lost frequency component. Each window was applied to the original waveform, with the result illustrating the trade-off between sharpness of peaks and decay of sidelobes. (c) shows a Hamming window. Note that this window never brings the signal to zero. (d) shows the Bartlett window, (e) shows the Hanning window, and (f) shows the Blackman window. For this spectral-separation example, the Blackman window is the best at bringing out the weaker term as a well defined peak.
Figure 4 — The significance of window selection is well illustrated by the Fourier transformation of two sine waves close to each other in frequency, but widely differing in amplitude. (a) shows the best case, matched end-point transform where the two signal frequencies that makeup the original waveform are clearly defined, one 2.2 Hz at 90 dB and the other 10.9 Hz at 46 dB. More typically, (b) shows the transform of the same waveform only with mismatched end-points. Note that the second peak is not even visible in this spectrum. The need for a window clearly exists. The remaining transforms illustrate the degree of success attained with various windows in suppressing spectral leakage and recovering the lost frequency component. Each window was applied to the original waveform, with the result illustrating the trade-off between sharpness of peaks and decay of sidelobes. (c) shows a Hamming window. Note that this window never brings the signal to zero. (d) shows the Bartlett window, (e) shows the Hanning window, and (f) shows the Blackman window. For this spectral-separation example, the Blackman window is the best at bringing out the weaker term as a well defined peak.
| Transform Type | Number of Points | |||||
| 512 | 1024 | 2048 | 4096 | 8192 | 16384 | |
| FFT | 0.3 | 0.6 | 0.9 | 1.4 | 2.6 | 7.3 |
| DFT | 1.3 | 2.0 | 3.3 | 5.6 | 12.6 | -- |
Table 1 — Elapsed computation time in seconds for various-point transforms. It should be mentioned that the DFT was calculated over a range of data points equal to one less than the number shown. This was done to ensure that the software would generate a DFT. If it is operating on a 2-to-the-nth-power number of data points (e.g., 1024), the software is "smart" enough to recognize that either an FFT or a DFT can be generated from this number of data points. Since a DFT means many more unnecessary calculations, the software will take the path of least calculations, resulting in an FFT. WinDaq is capable of transforming a maximum of 16,384 data points using an FFT, and 8,191 points using a DFT.
Time Series Generation Using The IFT
As with other bilateral transformations, such as rectangular to polar coordinates, the Fourier transformation works in both directions. If the power spectrum (as a function of frequency) were to be "run backward", the original signal would be, in principle, reconstructed as a function of time. This is known as the inverse Fourier transform (IFT). You might be questioning the purpose of an IFT if all it does is get you back to where you started. The beauty of the IFT lies in its ability to get you back to the time domain after the power spectrum has been edited in the frequency domain. This capability is very useful in power spectrum filtering applications. For example, in many cases it is desirable to examine a waveform without any "noise" present to distort the true nature of the signal. This can be done by applying high-pass, low-pass, band-pass, and notch filter functions to the power spectrum before performing the IFT. A high-pass filter will remove all unwanted frequency components less than a designated point on the power spectrum and a low-pass filter removes all unwanted frequency components greater than the designated point. A band-pass filter is a combination of high-pass and low-pass filters applied to isolate a narrow band of interest on the power spectrum. A notch filter removes the unwanted frequency component at the designated point. Figure 5 illustrates the kind of power spectrum editing possible in the frequency domain. Filtering operations can be a powerful feature in a Fourier analysis software package.
Other Fourier Analysis Software Issues
The needs of any Fourier analysis application are best served by a graphics based software package that allows fast power spectrum editing. In addition to the basic FFT, DFT, and IFT operations, the value of a Fourier analysis software package can be further enhanced by the extra "bells and whistles" that accompany it.
Software packages supporting waveform Fourier analysis should be capable of displaying the strength of a frequency component in either engineering units or relative magnitude (decibels) since converting power spectrum amplitude units can be a time consuming task.
Another issue is power spectrum resolution. Other than speed, resolution is the only other difference between a 512-point transform and a 16,384-point transform. A power spectrum always ranges from the dc level (0 Hz) to one-half the sample rate of the waveform being transformed, so the number of points in the transform defines the power spectrum resolution (a 512-point Fourier transform would have 256 points in its power spectrum, a 1024-point Fourier transform would have 512 points in its power spectrum, and so on). For example, if you wanted to see separate 20 and 21 Hz frequency components in the power spectrum of a complex waveform, a 512-point Fourier transform might not show these individual components clearly since its entire power spectrum is only divided into 256 equally spaced points and the desired frequencies are so close together. However, if the transform contained more points, it would be able to devote more points to the definition of closely spaced frequency components. The more the number of points in the transform, the better the frequency resolution.
(a) Original Waveform

(b) Power Spectrum of (a)

(c) Filtered Power Spectrum
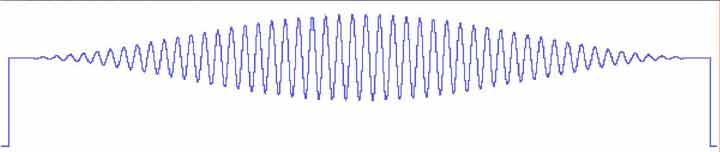
(d) IFT Result
Editing takes place in the frequency domain. The waveform shown by (a) is a 20 Hz signal containing undesirable 60 Hz noise. A 512-point FFT was used to generate its power spectrum shown by (b). While in the frequency domain, all undesirable frequency components greater than the 40 Hz corner frequency (including the 60 Hz noise) were edited out, or reduced to zero by applying a low pass filter as shown by (c). An IFT was then generated from this filtered power spectrum resulting in the pure 20 Hz waveform shown by (d). Note the bell-shaped appearance of the waveform. This is due to the application of a Hanning window, a solution to the spectral leakage dilemma inherent with the FFT. Note also how the Hanning window attenuates the signal to zero at the edges of the window. Had a DFT been applied, this attenuation would be eliminated and the 20 Hz signal would be displayed at its full amplitude from end to end.
A related issue is power spectrum magnification. The software under consideration should be able to display the entire power spectrum on one screen width regardless of the number of points in the transform. This is useful for spotting the overall trend of a spectrum. With magnification, the software should also allow you to select a portion of the power spectrum plot and examine it more closely with several magnification factors. A video standard of 1024 × 768 provides 1024 picture elements (pixels) of horizontal resolution. If a 512-point Fourier transform is performed, the 256 points generated by the transform fit nicely on a screen 1024 pixels wide. The same is true of a 1024-point transform, where a 1024 pixel wide screen is more than adequate to contain the 512 points generated by the transform. The problem arises when a transform larger than 2048 points is performed. Say an 8192-point Fourier transform is performed. The 4096 points generated by the transform is much wider than the 1024 pixel width of the screen. In order to get the entire power spectrum on one screen width, a compression factor (in this case, a factor of 4) must be applied. Magnification must then be applied to examine the spectrum at the full resolution of the 8192-point transform. Additionally, when a magnification factor is applied that prohibits the display of the entire power spectrum on a single screen width, the software should allow you to pan the entire plot one screen width at a time.
Yet another feature to consider is an export facility. Is it possible to export the coordinates defining an FFT plot to an ASCII file with the software you are considering? This feature allows you to reproduce the spectrum for use in other programs.
Does the software you are considering allow you to quickly see the results of each window on the same waveform? This can be a handy and time saving feature when experimenting with the different types of windows and the results each one delivers.
Finally, the software package should be capable of power spectrum smoothing. This is best implemented by a moving average utility. A moving average is accomplished by taking two or more data points from the spectrum, adding them together, dividing their sum by the total number of data points added, replacing the first data point with the average just computed, and repeating the steps with the second, third, and so on data points until the end of the data is reached. This simple averaging technique is used to attenuate random, small amplitude frequency spikes often encountered in a power spectrum plot.
References
1Ronald N. Bracewell, "The Fourier Transform," Scientific American, June 1989, pp. 86-95.


 View Cart
View Cart sales@dataq.com
sales@dataq.com 330-668-1444
330-668-1444